Question

IGMatch each equation on the left with the number and type of its solutions on the right.x² +9= 6xtwo complex (nonreal) solutionstwo real solutions4x² + 3x + 1 = 02x² - 4x = 1

Answer 1

0. one real solution.

,

1. two complex (nonreal) solutions.

,

2. two real solutions

1) In this problem, we don't actually need to solve these quadratic equations. We need to solve for the discriminant, and then analyze the results.

`\begin{gathered} a)\:x^2+9-6x=0\Rightarrow x^2-6x+9=0 \\ \Delta=(-6)^2-4(1)(9) \\ \\ \Delta=36-36 \\ \\ \Delta=0 \end{gathered}`

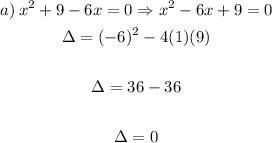
Since the discriminant yielded zero. Then we can tell for this one:

one real solution.

2) 4x²+3x+1=0

`\begin{gathered} \Delta=(3)^2-4(4)(1) \\ \\ \Delta=9-16 \\ \\ \Delta=-7 \end{gathered}`

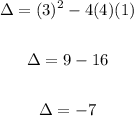
Note that -1 is lesser than zero. That means that this quadratic equation has two complex (nonreal) solutions.

3) 2x²-4x=1

`\begin{gathered} 2x^2-4x-1=0 \\ \\ \Delta=(-4)^2-4(2)(-1) \\ \\ \Delta=16+8 \\ \\ \Delta=24 \end{gathered}`

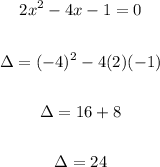
Since 24 is greater than zero, we can tell that this quadratic equation has two real solutions.

Thus, the answer:

0. one real solution.

,

1. two complex (nonreal) solutions.

,

2. two real solutions