Question

A point lies on AB and 3/10 the distance from A to B. Point A is located at (5, 10) and point B is located at (20, 25).What are the coordinates of this point?(9 1/2,14 1/2)(9 1/2, 20 1/2)(15 1/2,20 1/2)(15 1/2, 20 1/2)

Answer 1

The coordinates of the point that lies between the two points (x1, y1) and (x2, y2) at the ratio m1: m2 from the first point to the second point is

`x=\frac{m_{1_{}}x_2+m_2x_1_{}}{m_1+m_2}`
`y=(m_1y_2+m_2y_1)/(m_1+m_2)`

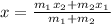
Since the point lies on 3/10 from points A and B, then

`\begin{gathered} m_1=3 \\ m_2=10-3=7 \end{gathered}`

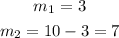
Since the coordinates of A are (5, 10) and B are (20, 25), then

`\begin{gathered} x_1=5,x_2=20 \\ y_1=10,y_2=25 \end{gathered}`

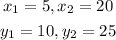
Substitute them in the rules above to find the coordinates of the point of division

`\begin{gathered} x=((3)(20)+(7)(5))/(3+7) \\ x=(60+35)/(10) \\ x=(95)/(10) \\ x=9(1)/(2) \end{gathered}`

`\begin{gathered} y=(3(25)+7(10))/(3+7) \\ y=(75+70)/(10) \\ y=(145)/(10) \\ y=14(1)/(2) \end{gathered}`

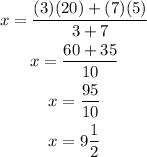
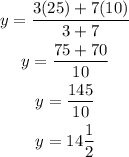
The coordinates of the point are (9 1/2, 14 1/2)

The answer is A