Question

25. In what base does 12+ 26b = 41b?

Answer 1

The operation is in base 7.

Step-by-step explanation

We are asked to determine in what base

`12_b+26_b=41_b`

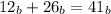
To do this, we just convert all of these to base 10

`\begin{gathered} 12_b=(1* b^1)+(2* b^0)=(1* b)+(2*1)=(b+2) \\ 26_b=(2* b^1)+(6* b^0)=(2* b)+(6*1)=(2b+6) \\ 41_b=(4* b^1)+(1* b^0)=(4* b)+(1*1)=(4b+1) \end{gathered}`

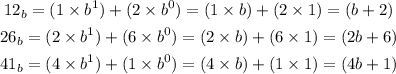
The equation can then be written in base 10 as

(b + 2) + (2b + 6) = (4b + 1)

b + 2 + 2b + 6 = 4b + 1

b + 2b + 2 + 6 = 4b + 1

3b + 8 = 4b + 1

We can rewrite this as

4b + 1 = 3b + 8

4b - 3b = 8 - 1

b = 7

Hope this Helps!!!