The given expression is
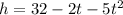
The ground is at h = 0, so
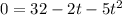
Now, we use the quadratic formula to find the solutions.
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where a = -5, b = -2, and c = 32.
![\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4\cdot(-5)\cdot(32)}}{2\cdot(-5)}=\frac{2\pm\sqrt[]{4+640}}{-10}=\frac{2\pm\sqrt[]{644}}{-10} \\ x=(2\pm25.38)/(-10) \\ x_1=(2+25.38)/(-10)=-2.7 \\ x_2=(2-25.38)/(-10)=2.34 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qisjmrfijuifkbs62xdl2go9ng1x79krz3.png)
In this case, just the positive solution makes sense.
Therefore, the ball takes 2.34 seconds to hit the ground.