a)
The outcomes of rolling a cube can be 1, 2, 3, 4, 5 or 6. From those outcomes, 2, 4 and 6 are even numbers. Then, 3 out of 6 outcomes are even numbers. The theoretical probability of getting an even number is:
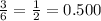
b)
From Mary's results, we can see that a 2 was rolled 9 times, a 4 was rolled 3 times and a 6 was rolled 3 times. The total amount of times that an even number was rolled, is 15. Then, the experimental probability of rolling an even number according to Mary's results, is:
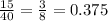
c)
With a large number of trials, the experimental probability approaches the theoretical probability. Then, with a large number of rolls, there might be a difference between the experimental an theoretical probabilities, but the difference should be small.
Therefore, the answers are:
a) Theoretical probability of rolling an even number: 0.500
b) Experimental probability of rolling an even number: 0.375
c) With a large number of rolls, there might be a difference between the experimental an theoretical probabilities, but the difference should be small.