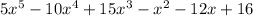Question

Simplify and put in standard form: (12x5 + 10x3 - 8x4 - 6x +4) - (7x5 + 2x4 - 12+6x – 5x3 + x2 )

Answer 1

Step-by-step explanation:

First we have to order the polynomials between parenthesis:

`(12x^5-8x^4+10x^3-6x+4)-(7x^5+2x^4-5x^3+x^2+6x-12)^{}`

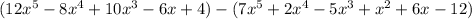
Then we have to eliminate the parenthesis by multiplyin each term of the second polynomial by -1:

`12x^5-8x^4+10x^3-6x+4-7x^5-2x^4+5x^3-x^2-6x+12`

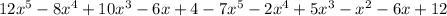
Now we have to add like terms:

`\begin{gathered} (12x^5-7x^5)+(-8x^4-2x^4)+(10x^3+5x^3)+(-x^2)+(-6x-6x)+(4+12) \\ (5x^5)+(-10x^4)+(15x^3)+(-x^2)+(-12x)+(16) \end{gathered}`

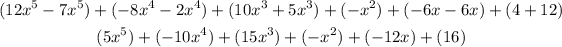
Finally we eliminate the parenthesis of each term

Answer:

`5x^5-10x^4+15x^3-x^2-12x+16`