Question

Select all of the equations for which x= 4 is a solution

Answer 1

The correct options here are; A, B,

Here, we want to select the equations where x = 4 is a solution

To do this, we have to solve the equations

We proceed as follows;

`\begin{gathered} a)(16)/(x)=\text{ 4} \\ 16\text{ = 4}* x \\ 4x\text{ = 16} \\ x\text{ = }(16)/(4)\text{ = 4} \end{gathered}`

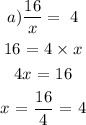
x = 4 is a solution to this, so, we select it

`\begin{gathered} b)x^2\text{ = 16} \\ x\text{ = }\sqrt[]{16} \\ x\text{ = + 4 or -4} \end{gathered}`

x= 4 is also a solution, so we select it

`\begin{gathered} c)\text{ 33-x = 37} \\ 33-37\text{ = x} \\ x\text{ = -4} \end{gathered}`

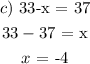
x = 4 is not a solution here, so we do not select it

`\begin{gathered} d)\text{ 16 = 4x} \\ x\text{ = }(16)/(4) \\ x\text{ = 4} \end{gathered}`

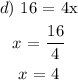
x = 4 is a solution here, so we select it

`\begin{gathered} e)\text{ 2(2+x) = 8} \\ 2+x\text{ = }(8)/(2) \\ 2+x\text{ = 4} \\ \text{ x = 4-2 = 2} \end{gathered}`

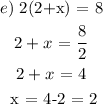
x = 4 is not a solution here, so we do not select it