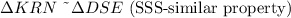We will investigate how to determine the similarity off two triangles under the SSS property.
We are given two triangles in the first part. We will first state the SSS property of similar triangles:
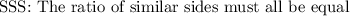
Before we start with the ratios. We need to identify the similar sides of the two triangles. Longest side of one triangle is similar to the longest side of the other, Middle side of one triangle is similar to the middle side of the other, and smallest side of one triangle is similar to the smallest side of the other.
We can express the similar sides statements as follows:
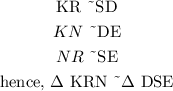
Now we will verify the hypothesis of similar sides by taking ratios of similar sides as follows:
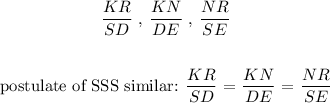
We will plug in the respective side values and determine the ratios:
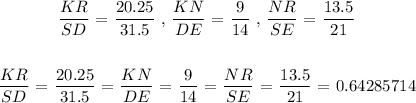
We see that the calculated values of the ratios of similar sides are ALL equal! Therefore, the triangles: