Question

Sec(3x - 15) = csc(14x + 3)

Answer 1

To solve the equation for x we have to express the equation in term of only one trigonometric function, and for doing this we use the identies.

`\begin{gathered} \sec (x)=(1)/(\cos(x)) \\ \csc (x)=\frac{1}{\text{ sin(x)}} \end{gathered}`

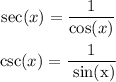
so in our problem would be:

`\begin{gathered} \sec (3x-15)=\csc (14x+3) \\ \sec (3x-15)-\csc (14x+3)=0 \\ (1)/(\cos(3x-15))-\frac{1}{\text{sin}(14x+3)}=0 \end{gathered}`

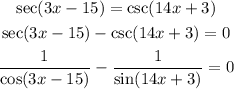
now we can do de subtraction:

`\frac{\text{sen}(14x+4)-\cos (3x-15)}{\cos (3x-15)\text{sin}(14x+3)\text{ }}=0`

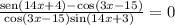
then we can use the identity of adition of angles:

`\begin{gathered} \text{Sin(}14x+4)=sin(14x)\cos (4)+sin(4)\cos (14x) \\ \cos (3x-15)=\cos (3x)\cos (15)+\text{ sin(3x)sin(15)} \end{gathered}`

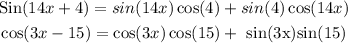
and replace that in our problem:

`\begin{gathered} \frac{\text{sin}(14x)\cos (4)+\text{sin}(4)\cos (14x)-\cos (3x)\cos (15)-\text{sin}(3x)\text{sin}(15)}{(\cos (3x)\cos (15)+\text{sin}(3x)\text{sin}(15))(\text{sin}(14x)\cos (4)+\text{sin}(4)\cos (14x)} \\ =0 \end{gathered}`

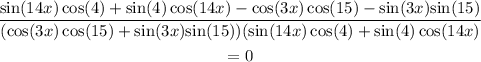
now we can simplify the expression:

`\begin{gathered} \text{sin}(14x)\cos (4)+\text{sin}(4)\cos (14x)-\cos (3x)\cos (15)-\text{sin}(3x)\text{sin}(15) \\ =\text{ cos(3x)cos(15)sin(14x)cos(4)+cos(3x)cos(15)sin(4)cos}(14x) \\ +\text{sin}(3x)\text{sin}(15)\text{sin}(14x)\cos (4)+\text{sin}(3x)\text{sin}(15)sin(4)\cos (14x) \end{gathered}`

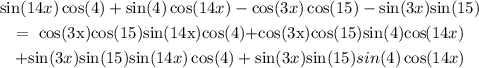
Finaly, weput all the expressions with x to the left of the equation:

`\begin{gathered} \text{sin}(14x)\cos (4)+\text{sin}(4)\cos (14x)-\cos (3x)\cos (15)-\text{sin}(3x)\text{sin}(15) \\ -\text{cos(3x)cos(15)sin(14x)cos(4)}-\text{cos(3x)cos(15)sin(4)cos}(14x) \\ -\text{sin}(3x)\text{sin}(15)\text{sin}(14x)\cos (4)-\text{sin}(3x)\text{sin}(15)sin(4)\cos (14x)=0 \end{gathered}`

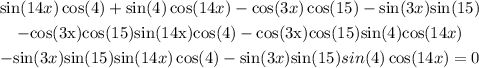
and there is not posible to simplify this expresion