The line PQ and the line tangent to PQ at point Q are perpendicular lines, since P is the circle center and Q is on the circle.
Perpendicular lines have the following relation about their slopes:
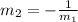
Comparing the equation of line PQ with the slope-intercept form of the linear equation (y = mx + b), we have a slope m = 2/5.
Therefore the slope of the tangent line is:

Now, let's put the equation in the standard form:
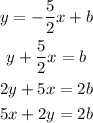
The only option with "5x + 2y" on the left side is the third option.