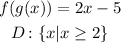Step 1. The two functions we have are:
![\begin{gathered} f(x)=2x^2 \\ g(x)=\sqrt[]{x-2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/25vrhcvriy4uq8pj6f8skteky21j5i4z9h.png)
And we are asked to find the composite function f(g(x)) and the domain.
Step 2. The function that we need to find is:

To find this, we substitute g(x) into the x value of f(x):
![f(g(x))=2(\sqrt[]{x-2})^2-1](https://img.qammunity.org/2023/formulas/mathematics/high-school/p27su35ry4mgsvd4xrh2iayiniygrudxbk.png)
Step 3. Simplifying:
The square root and the power of two cancel each other
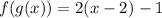
Distributing the multiplication by 2:
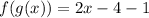
Combining the like terms:
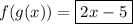
Step 4. Find the domain. The domain is the set of possible values that the x variable can take.
Remember the two original functions:
![\begin{gathered} f(x)=2x^2 \\ g(x)=\sqrt[]{x-2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/25vrhcvriy4uq8pj6f8skteky21j5i4z9h.png)
for f(x) x can take any value. But for g(x) the square root cannot be a negative number, therefore, x-2 has to be equal to or greater than 0:
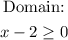
Solving for x:
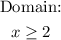
This domain also applies to the composite function f(g(x)), and it can be written as follows:
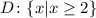
Answer: Option four