Let's take a look at what's going on:
We know the perimeter of the playground (the sum of the lenght of its sides) has to be 460ft. Thereby,
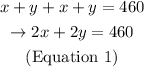
And the area has to be at least 8600 square ft. Remember that the are of a rectangle is the multiplication between the lenght of its base and the lenght of its height. Therefore,
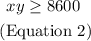
Now, let's clear x from (Equation 1) and substitute in (Equation 2). This will be our Algebraic method
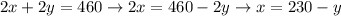
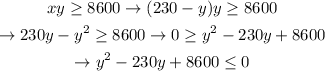
We get a quadratic inequality. We'll solve it as following:
0. Complete the square:
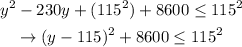
2. Simplify:
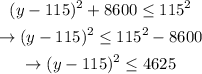
Remember that
![a^2\le b\rightarrow-\sqrt[]{b}\le a\le√(b)](https://img.qammunity.org/2023/formulas/mathematics/college/sfmr0linennmc5nu1kyj44z6zsibocsb2s.png)
3. Use this property:
![\begin{gathered} (y-115)^2\le4625 \\ \rightarrow-\sqrt[]{4625}\le y-115\le\sqrt[]{4625} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k56pwqg1l0jxqgo8adul038og2zbmwwpmd.png)
4. Add 115:
![-\sqrt[]{4625}+115\le y-115+115\le\sqrt[]{4625}+115](https://img.qammunity.org/2023/formulas/mathematics/college/bxrycxdl5kl8zupss3dryhyo39f8svtboa.png)
5. Solve:
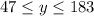
Now we know that the height can be between 115ft and 183ft. We've already cleared x, so let's substitude for both the values we've calculated:
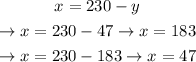
Thereby, we've calculated the lenght (x) of the playground has to be between 47ft and 183ft