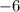Question

Reduce the rational expression to lowest terms. If it is already in lowest terms, enter the expression in the answer box. Also, specify any restrictions on the variable.a²-36/5a + 30Rational expression in lowest terms:Variable restrictions for the original expression: a

Answer 1

The expression is given to be:

`(a^2-36)/(5a+30)`

From the numerator, using the difference of two squares, we have:

`a^2-36=a^2-6^2=(a-6)(a+6)`

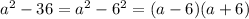
From the denominator, by factorization, we have:

`5a+30=5(a+6)`

Therefore, the expression becomes:

`\Rightarrow((a-6)(a+6))/(5(a+6))`

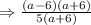
Cancel out common terms in the denominator and numerator. The simplified expression will be:

`\Rightarrow(a-6)/(5)`

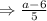
From the original expression, the variable restriction will be at:

`\begin{gathered} 5a+30=0 \\ Solving \\ 5a=-30 \\ a=-(30)/(5) \\ a=-6 \end{gathered}`

The restriction is:

`-6`