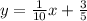Question

line g has an equation of y=-10x-2. Line h, which is perpendicular to line g, includes the point (4,1). what is the equation of line h?

Answer 1

The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

Given the equation of the line "g":

`y=-10x-2`

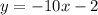
You can identify that:

`\begin{gathered} m_g=-10 \\ b_g=-2 \end{gathered}`

By definition the slopes of perpendicular lines are opposite reciprocals. Then, the slope of the line "h" is:

`m_h=(1)/(10)`

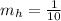
Knowing a point on the line "h" and its slope, you can substitute them into the equation

`y=m_hx+b_h`

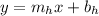
And solve for the y-intercept:

`\begin{gathered} 1=(1)/(10)(4)+b_h \\ \\ 1=(2)/(5)+b_h \\ \\ b_h=(3)/(5) \end{gathered}`

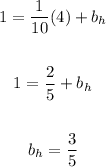
Then, the equation of the line "h" is:

`y=(1)/(10)x+(3)/(5)`