Question

4. Solve the system of equations (show ALL work!). What is the value of y?– 5x + 3y =- 334x + 3y =- 6A. 39B. 13C. 3D. -6

Answer 1

Step 1. The system of equations we have is:

`\begin{gathered} -5x+3y=-33 \\ 4x+3y=-6 \end{gathered}`

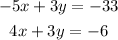
And we are required to find the value of y.

Step 2. To solve this system of equations, we will use the equal values method. This method consists in finding two equal expressions and equaling them into one equation.

For this, we solve for 3y in the two given equations:

`\begin{gathered} 3y=-33+5x \\ 3y=-6-4x \end{gathered}`

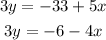
Step 3. Now we make the two expressions for 3y equal to each other:

`-33+5x=-6-4x`

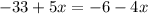
Step 4. Solve for x.

To solve for x, move all of the terms that contain x to one side of the equation, and all of the numbers to the opposite side:

`5x+4x=-6+33`

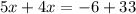
Combine the like terms:

`9x=27`

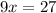
Divide both sides by 9:

`\begin{gathered} x=(27)/(9) \\ \downarrow\downarrow \\ x=3 \end{gathered}`

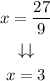
Step 5. Now that we know the value of x is x=3, we substitute this value into the first equation:

`\begin{gathered} -5x+3y=-33 \\ -5(3)+3y=-33 \end{gathered}`

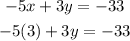
And solve for y:

`\begin{gathered} -15+3y=-33 \\ 3y=-33+15 \\ 3y=-18 \\ y=-(18)/(3) \\ \boxed{y=-6} \end{gathered}`

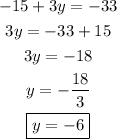
Answer:

D. -6