GIVEN
A compound interest account with a principal of $9500 accumulating to $11346 in 7 years, compounded annually.
TO FIND
The interest rate.
SOLUTION
The compound interest formula is given to be:
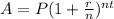
where
A = final amount
P = initial principal balance
r = interest rate
n = number of times interest applied per time period
t = number of time periods elapsed.
From the question, the following parameters are seen:
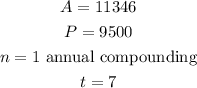
Therefore:
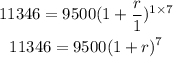
Solve for r:
![\begin{gathered} (1+r)^7=(11346)/(9500) \\ 1+r=\sqrt[7]{(11346)/(9500)} \\ r=\sqrt[7]{(11346)/(9500)}-1 \\ r=0.02569 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/w9iqfhm4pcjvyx8m2u5u388s5qwb2t6c7f.png)
Multiply by 100:
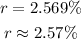
ANSWER
The interest rate required to get a total amount of $11,346.00 from compound interest on a principal of $9,500.00 compounded once per year over 7 years is 2.57% per year.