The greatest common factor (GCF) of the monomials is obtained as follows:
- First, we have to find the GCF of the constant coefficients of each monomials, that is the GCF of 6, 2, and 2
To do this, we have to write out the prime factorization of each number and then select the common prime number, as follows:
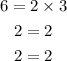
Thus the GCF of the constant coefficients of the monomials is 2
- Second, we have to expand the variables of each monomial and then select the variables that occur the most, as follows:
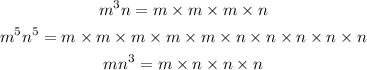
From the above, we can see that "m" occurs at least once, and "n" occurs at least once also.
Therefore the GCF of the monomials (without considering their constant coefficients) is:
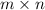
- Finally, we now combine the two GCFs we have obtained so far, in order to obtain the overall GCF of the monomials, as follows:
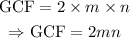
Thus, the greatest common factor of the monomials given in the question is 2mn