To graph the parabola we can give any numbers for x and then solve for y, or we can find the vertex and then go to either way.
0. Finding the vertex.
The x value of the vertex's coordinate can be calculated as follows:
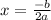
where a and b represent the coefficients of the equation of the parabola in the form:

As our parabola is:
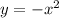
we can see that a = -1 and b = 0. Replacing this in the formula for the x coordinate:

We have to replace this value in the equation:
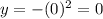
Then the vertex can be found in (0,0).
Now we have to find different coordinates in each side to graph the parabola by giving arbitrarily numbers to x and evaluating them in the equation.
• x = 1
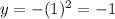
Then the coordinate, in this case, is (1, -1)
• x = -2

The coordinate, in this case, is (-2, -4).
• x = 3
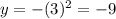
The coordinate is (3, -9).
• x = -4
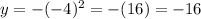
The coordinate is (-4, -16).
We can keep choosing any value for x to find y and get the coordinate in need be.
Answer:
• (0,0)
,
• (1, -1)
,
• (-2, -4)
,
• (3, -9)
,
• (-4,-16)