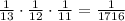Question

There are thirteen drink choices listed on a poll. The poll wants to see what drinks are most liked. What is the probability that you will guess the first, second, and third top drinks correctly in order?Write your answer as an exact fraction which is reduced as much as possible.

Answer 1

The probability of correctly choosing the top 3 ranked drinks is given by the product of three different probabilities: the probability of correctly ordering the first one, the same probability but for the second one and that of the third one. Since we have a total of 13 drinks, the probability of correctly ranking one of them is one out of 13:

`(1)/(13)`

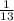
So we have 1/13 chances of correctly ranking one of the top 3 drinks. Let's assume we did it, now we have 12 non-ranked drinks left to choose. Then, the probability of correctly ranking one of them is:

`(1)/(12)`

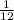
Again, let's assume that we chose another one from the top 3. Now, with 11 non-ranked drinks the probability of correctly ranking one of them is:

`(1)/(11)`

With all these three probabilities we can assure that the probaility of correctly ranking the top 3 drinks is given by:

`(1)/(13)\cdot(1)/(12)\cdot(1)/(11)=(1)/(1716)`