SOLUTION
Given the pyramid with a square base in the image, the following are the solution steps wo find the surface area.
Step 1: Describe the formula of the surface area of the pyramid
The pyramid consists of a square base and 4 triangles, therefore the surface area of the pyramid will be the area of the square base added to the areas of the 4 triangles.
Step 2: To get the surface area of the pyramid, we calculate the area of the square base

Step 3: We calculate the area of the 4 triangles
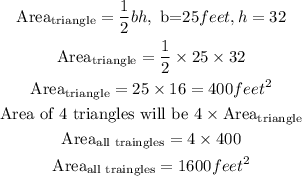
Step 4: Calculate the surface area by following the instruction in Step 1:
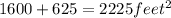
Hence, the surface area of the pyramid equals 2225 square feet.
Question b: Surface area of the metal soup can
The metal soup can has the shape of a cylinder, therefore the surface area will be:
![\begin{gathered} SA=2\pi r^2+2\pi r^{}h,r=5,h=20\operatorname{cm} \\ SA=(2*\pi*5*5)+(2*\pi*5*20) \\ SA=157.0796327+628.3185307 \\ SA=785.3981634 \\ SA\approx785.39816\operatorname{cm} \end{gathered}]()
Hence, the surface area of the metal soup can equals 785.39816 square cm.
Question c: Surface area of the ice cream cone with an open top
It can be seen from the image that the height is missing from the cone.
Surafce area of a cone with an open top means we exclude the area of the circular surface:
![\begin{gathered} SA=\pi rl,l=16.6\operatorname{cm},r=(9.4)/(2)=4.7\operatorname{cm} \\ SA=\pi*4.7*16.6 \\ SA=245.1070588 \\ SA\approx245.107\operatorname{cm} \end{gathered}]()
Hence, the surface area of the ice cream cone can equals 245.107 square cm.