Question

QUESTION 3 1 POINTWhich of the numbers given are rational?Select all that apply.Previous29.6476129.42664√16930.760520...24.95568

Answer 1

Given: The numbers are provided.

To find: Whether the numbers are rational numbers or not?

Explanation:

A number that can be expressed in the form of p/q is called a rational number.

Let us check the first number 29.64761 , it is a rational number since we can express it as

`(2964761)/(100000)`

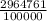
The next number is 29.42664, it is also a rational number . Since, it can be expressed as

`(2942664)/(100000)`

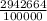
The next number is

`√(169)`

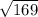
the value of of which is

`√(169)=13`

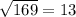
it is a rational number since 13 can be expressed as

`(13)/(1)`

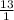
The next number is 30.760520....

It is not a rational number since it is non-terminating and the non-terminating decimals are not repeating also.

therefore, 30.760520.... is not a rational number.

the last number

`24.955\bar{68}`

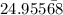
it is a rational number since the decimals are repeating. As we can see the term 68 above it has bar so it will keep on repeating.

Therefore, the number is a rational number.

Final Answer: The rational numbers are 29.64761, 29.42664,

`√(169)`

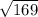
and

`29.955\bar{68}`