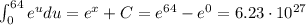We have to solve the integral:
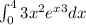
(Note: the editor does not let write x^3 as the exponent of e)
We will have to do a substitution of variables in order to simplify the solution.
For example, we can see that the derivative of x^3 is 3x^2, that is the factor that multiplies the exponential function. This tells us a clue about a possible substitution.
So we will try the following substitution:
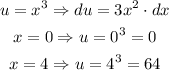
Then:
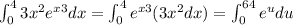
We can solve this integral as: