Question

Bob deposited $2000 in a saving account in which interest is compounded continuously. After 21 years, he has $5000 in this account.(1) What is the annual rate of interest? (Round your answer to one decimal place.) % Tries 0/99(2) How long does it take for his money to double? (Round your answer to two decimal places.) years Tries 0/99

Answer 1

We have to use the compount interest formula

`\begin{gathered} A=P(1+r)^t \\ (A)/(P)=(1+r)^t \\ \\ \sqrt[t]{(A)/(P)}=\sqrt[t]{(1+r)^t}^ \\ \\ r=\sqrt[t]{(A)/(P)}\text{ - }1 \\ \\ r=\sqrt[21]{(5000)/(2000)}\text{ - }1 \\ r=0.04459 \\ r=4.45\%=4.5\% \end{gathered}`

A is the total amount

P is the principal amount

r is the interest annual rate, which is the unknown variable and t is the nnumber of yeaers

That would be the formula for the r. Let's find it then

For a the annual rate of interest is 4.5%

2) Now, we have the r, we can find the number 2 which is how long for it to double, so we have to find t.

`\begin{gathered} A=P(1+r)^t \\ \\ 4000=2000(1+0.045)^t \\ \\ (4000)/(2000)=(1.045)^t \\ 2=1.045^t \\ \log_(1.045)2=t \\ \\ t=15.747=15.75\text{ years} \end{gathered}`

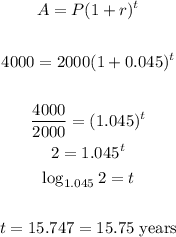
So, for it to double it takes 15.75 years.