The area of a regular pyramid is:
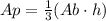
Where:
Ap = Area of the regular pyramid
Ab = Area of the basis
h = height of the pyramid
And, Ab is:
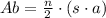
Where:
n = number of sides of the polygon
s = measure of the side of the polygon
a = apothem
So, to solve this question, follow the steps below.
Step 01: Find Ab.
To find Ab, let's extract the info from the problem:
n = 6
s = 12 cm.
a = 10.4 cm.
Then,
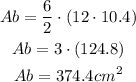
Step 02: Use Ab to find Ap.
From the problem:
h = 36 cm.
Then,
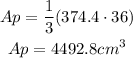
Answer: A) 4492.8 cm³.