Question

From the roof of a building, the angles of depression of the top and the bottom of a utility pole are 33 degrees and 52 degrees. Find the height of the building if the pole is 27 m high

Answer 1

Given:

From the roof of a building, the angles of depression of the top and the bottom of a utility pole are 33 degrees and 52 degrees.

To find:

Find the height of the building if the pole is 27 m high.

Solution:

Let the height of the building be x m. So, the figure for the given question is as follows:

From the figure, it is clear that:

`\begin{gathered} \tan52=(x)/(y) \\ 1.28=(x)/(y) \\ y=(x)/(1.28) \end{gathered}`

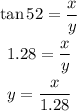
And from the second triangle:

`\begin{gathered} \tan33=(x-27)/(y) \\ 0.65=(x-27)/((x)/(1.28)) \\ 0.65((x)/(1.28))=x-27 \\ 0.65x=1.28x-34.56 \\ -0.63x=-34.56 \\ x=(-34.56)/(-0.63) \\ x=54.86 \end{gathered}`

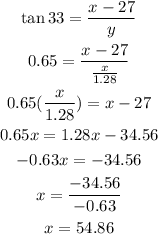
Thus, the height of the building is 54.86 m.