Question

I need help answer and solving problem his This is a practice problem from my trigonometry prep guide

Answer 1

We have the following diagram

First, we find the distance from Corey to the tree (x). We use the trigonometric tangent identity:

`\begin{gathered} \tan 68=(opposite)/(adjacent) \\ \tan 68=(80)/(x) \end{gathered}`

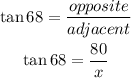
And solve for x:

`x=(80)/(\tan 68)=32.32`

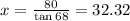
So, x = 32.32 ft

Now Corey moves back to watch the very same tree at an elevation angle of 41°. The tree has the same height, we find y:

`\begin{gathered} \tan 41=(80)/(y) \\ y=(80)/(\tan 41) \\ y=92.03 \end{gathered}`

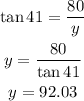
This is y = 92.03 ft

We can know the distance Corey step back by subtracting both distances:

`92.03-32.32=59.71`

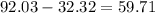
Answer: 59.71 ft