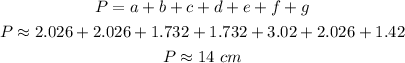Each letter represents one side of a right triangle.
We can find the length of side c as follows:
![\begin{gathered} \sin (60\degree)=(1.5)/(c) \\ c=(1.5)/(\sin(60\degree)) \\ c=\frac{1.5}{\frac{\sqrt[]{3}}{2}} \\ c\approx1.732\text{ }cm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hb04aywltvbj3wwwhjbuu934kt8flkj2e4.png)
Sides c and d are congrent, then:
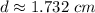
Applying the Pythagorean theorem to the triangle formed by sides c = 1.732, h, and the side of 1.5 cm, we get:
![\begin{gathered} 1.732^2=1.5^2+h^2 \\ 3=2.25+h^2 \\ 3-2.25=h^2 \\ \sqrt[]{0.75}=h \\ 0.866\text{ }cm\approx h \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/53524onafk4dv40yw8oopy29pgsvxbi6r4.png)
Applying the Pythagorean theorem to the triangle formed by sides 1.5 cm, d, and i, the same result is got, then:
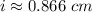
We can find the length of side e as follows:
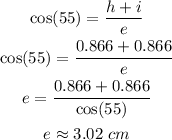
Applying the Pythagorean theorem, we can find the length of side j as follows:
![\begin{gathered} e^2=j^2+(h+i)^2 \\ 3.02^2=j^2+(0.866+0.866)^2 \\ 9.1204=j^2+3 \\ 9.1204-3=j^2 \\ \sqrt[]{6.1204}=j \\ j\approx2.474\text{ }cm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8tfn83522hyy7j2ffbefbh08723gyxsavg.png)
We can find the length of side b as follows:
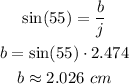
We can find the length of side l as follows:
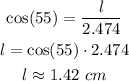
Considering that sides k and j are congruent, if we would apply the Pythagorean theorem to triangles with sides b, l, j, and a, l, k, we will conclude that sides a and b are congruent, then:
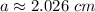
Sides a, f, g, l form a rectangle, then f and a are congruent, and l and g are also congruent, that is,
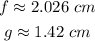
Finally, the perimeter of the figure shown is: