This is our rectangle:
We know that the area of a rectangle is it's length times it's width:
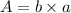
The problem says that one side is 12ft longer than 3 times the other side, so if a is the shorter side:
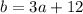
And we know that the area is 135ft². If we replace this and the expression for b into the equation for the area we can clear a and then find b:

Note that we got a 2 degree equation. We can solve it this way:
![\begin{gathered} 0=Ax^(2)+Bx+C \\ x=\frac{-B\pm\sqrt[]{B^(2)-4AC}}{2A} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nkz9gfov2bqhads4661sflh6aa1h33tsgr.png)
In our equation we have that A=3, B=12 and C=135 (and instead of x we have a):
![\begin{gathered} a=\frac{-B\pm\sqrt[]{B^2-4AC}}{2A} \\ a=\frac{-12\pm\sqrt[]{12^2+4\cdot3\cdot135}}{2\cdot3}=\frac{-12\pm\sqrt[]{144^{}+1620}}{6}=\frac{-12\pm\sqrt[]{1764}}{6}=(-12\pm42)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/z5fclbbcy45e11l0ngzlbmnj6o6rx5jmhl.png)
One of these results will be negative, but since a is the size of the side of a rectangle we don't want a negative number, so we'll keep the positive result:
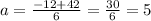
So we got that side a = 5 feet
Then we find b with the expression:
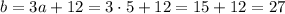
Side b = 27 feet