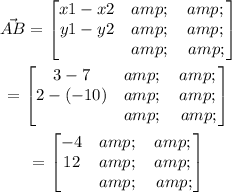Given:
The coordinates of point A,( x1, y1)=(3, 2)
The coordinates of point B, (x2, y2)=(7, -10).
The displacement vector that moves from point A onto B can be found as,
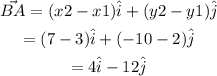
Hence, the displacement vector tha moves point A onto B is,
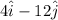
The displacement vector that moves point B onto A can be found as,
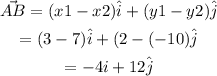
The displacement vector BA can be drawn as,
The displacement vector AB can be drawn as,
The displacement vector from point A onto B can be found as,
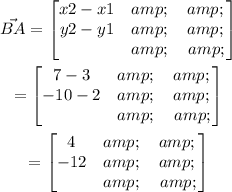
The displacement vector from point B onto A can be found as,