We can find the value of x by using Exterior Angle property:
Exterior Angle:
The exterior angle of a triangle is the angle formed between one side of a triangle and the extension of its adjacent side.
So, in the given figure we hvae exterior angle : BAD
Property of Exterior Angle:
The exterior angle theorem states that the measure of each exterior angle of a triangle is equal to the sum of the opposite and non-adjacent interior angles.
So, from the property :
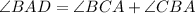
Now, substiute the given values of angle from the given figure:
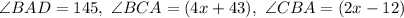
thus,
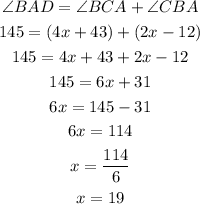
So, we get x = 19
Answer : x = 19