Answer: 5.89 g of Cu could be obtained from the reaction
Step-by-step explanation:
The question requires us to determine the amount of copper formed, given the unbalanced chemical equation and the amounts of reactants used.
The following information was provided by the question:
- chemical equation:
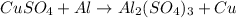
- amount of CuSO4: 20.0 ml of 1.5 M solution
- amount of Al: 2.50g
To solve this problem, we'll need:
1) balance the chemical equation;
2) calculate the amount of reactants in number of moles;
3) determine the limiting reactant;
4) calculate the amount of Cu produced.
1) Balancing the chemical equation
We can start balancing the chemical equation from Al: there is 1 Al atom on the left side and 2 Al atoms on the right side, thus we can adjust the coefficient of Al from 1 to 2:
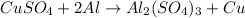
Next, we can adjust the amount of (SO4)2- ions: there are 3 ions on the right side and 1 on the left side, thus we can adjust the coefficient of CuSO4 from 1 to 3:
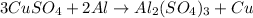
Now, we need to adjust the coefficient of Cu from 1 to 3 to fix the amount of Cu on both sides. The balanced chemical equation can be written as:

2) Determining the number of moles of reactants:
We can determine the number of moles of CuSO4 as:
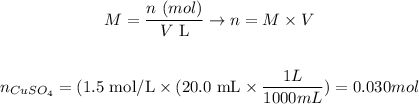
where n is the number of moles, M is the molarity of the solution and V is the volume of solution.
And the number of moles of Al can be determined as (the atomic mass of Al is 26.98 amu):

Therefore, 0.030 and 0.0927 moles of CuSO4 and Al, respectively, were used in the reaction.
3) Determining the limiting reactant
From the balanced chemical equation, we can see that 3 moles of CuSO4 are necessary to react with 2 moles of Al. Thus, we can write:
3 mol CuSO4 ------------------------- 2 mol Al
Using this stoichiometric relation, we can determine the amount of Al that would be necessary to completely react with 0.030 moles of CuSO4:
3 mol CuSO4 ------------------------- 2 mol Al
0.030 mol CuSO4 ------------------ x
Solving for x, we have that 0.020 moles of Al would be necessary. Since the actual amount of Al used (0.0927 mol) is greater than the necessary amount (0.020 mol), we can say that Al is the excess reactant and CuSO4 is the limiting reactant.
4) Calculating the amount of Cu produced
Now that we know the limiting reactant (CuSO4), we can determine how much Cu would be produced in the reaction.
From the balanced chemical equation, we know that 3 moles of CuSO4 are necessary to produce 3 moles of Cu. Thus, we can write:
3 mol CuSO4 -------------------- 3 mol Cu
0.0927 mol CuSO4 ----------- y
Solving for y, we have that 0.0927 moles of Cu would be produced.
The atomic mass of Cu is 63.55 amu, thus we can calculate the mass of Cu that corresponds to 0.0927 moles as:
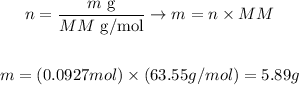
Therefore, 5.89 g of Cu could be obtained from the reaction.