Question

in 1 hr a plane can travel 440 mi into the wind and 480 mi with the wind. find the wind speed and the rate of the plane in still air.

Answer 1

So we have a plane that in 1 hour travels 440 miles going against the wind and 480 miles when it travels in the same direction as the wind. Dividing the distance by the time gives us the rate of the plane. The rate of the plane into the wind is then 440 mi/h whereas the rate with the wind is 480 mi/h. Now, the rate of the wind affects that of the plane because it's flying in the air. When we measure the rate of the plane travelling with the wind we are actually measuring the rate of the plane in still air (v) plus the rate of the wind (w) and that's equal to 480 mi/h. Analogously when we measure the rate of the plane going against the air we are measuring the rate of the plane in still air (v) less the rate of the wind (w) and that's equal to 440 mi/h. So basically we have two equations that relate the rate of the plane in still air and the rate of the wind:

`\begin{gathered} v+w=480 \\ v-w=440 \end{gathered}`

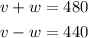
If we add w to both sides of the second equation we get:

`\begin{gathered} v-w+w=440+w \\ v=440+w \end{gathered}`

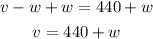
Then we replace v with this expression in the first equation:

`\begin{gathered} v+w=480 \\ 440+w+w=480 \\ 440+2w=480 \end{gathered}`

Then we substract 440 from both sides:

`\begin{gathered} 440+2w-440=480-440 \\ 2w=40 \end{gathered}`

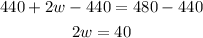
Then we divide both sides by 2:

`\begin{gathered} (2w)/(2)=(40)/(2) \\ w=20 \end{gathered}`

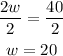
Now we use this value in the expression for v we found before:

`\begin{gathered} v=440+w \\ v=440+20=460 \end{gathered}`

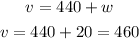
Then the wind speed is 20 mi/h and the rate of the plane in still air is 460 mi/h.