Question

Find each quotient. All final answers must be in simplest form.56x4y5 - 49x3y6 - 35x2y3 / 7x?y2 =A8x^2y^3 - 7y^4 - 5yB8x^2 y^3 - 7xy^4 + 5yC 8x^2y^3 - 7xy^4 - 5yD 8x^2y^3 + 7xy^4 - 5y

Answer 1

Option C is correct

8x²y³ - 7xy⁴ - 5y

Step-by-step explanation

The equation to be solved or reduced is

(56x⁴y⁵ - 49x³y⁶ - 35x²y³)/7x²y²

More properly written, the equation is

`(56x^4y^5-49x^3y^6-35x^2y^3)/(7x^2y^2)`

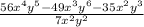
To solve this, we will break the division down and have each term carry the denominator and use the laws of indices to reduce the powers

`\begin{gathered} (56x^4y^5-49x^3y^6-35x^2y^3)/(7x^2y^2) \\ =(56x^4y^5)/(7x^2y^2)-(49x^3y^6)/(7x^2y^2)-(35x^2y^3)/(7x^2y^2) \\ =(56)/(7)x^(4-2)y^(5-2)-(49)/(7)x^(3-2)y^(6-2)-(35)/(7)x^(2-2)y^(3-2) \\ =8x^2y^3-7x^1y^4-5x^0y^1 \\ \text{Note that} \\ x^0=1 \\ x^1=x \\ y^1=y \\ 8x^2y^3-7x^1y^4-5x^0y^1 \\ =8x^2y^3-7xy^4-5^{}y^{} \end{gathered}`

Hope this Helps!!!