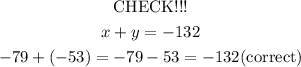Let the smaller number =x
Let the larger number = y
The first sentence states that the sum of the numbers is -132

The second sentence stated that twice the smaller number is one more than the larger number

Solving simultaneously, let's make x the subject of the formula in Eqn 1

Substitute eqn 3 in eqn 2 we will have ,

to find x substitute y=-53 in eqn 3
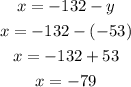
Therefore,
The numbers are -79 and -53