SOLUTION
Write out the equation given

The zeros of the polynomial is obtain by equating the polynomial to zero.
Hence
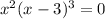
Equate each product to zero, we have

The zeros of the polynomial are
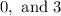
The zeros of the polynomials is 0 and 3
the multiplicity of multiple zeros is the number of times the zeros of the polynomial occur which is obtain from the degree of each terms in the polynomial.
Hence
![\begin{gathered} x^2 \\ \operatorname{mean}s\text{ x=0 occurs twice} \end{gathered}]()
Then
x =0 has the multiplicity of 2
For
![\begin{gathered} (x-3)^3 \\ \operatorname{mean}s\text{ (x-3) occurs thrice} \end{gathered}]()
x = 3 has a multiplicity of 3