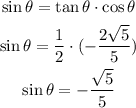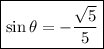Given an angle θ in standard position passing through (x, y), the following relationship stands:
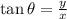
Our angle has a terminal side that passes through (-6, -3). Since both x and y are negative, the angle lies in quadrant III where the sine and the cosine are negative.
Substituting the given values:

Now we use the following identity:
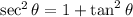
Substituting:

The secant is also negative in quadrant III, so:
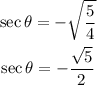
The cosine is the reciprocal of the secant:
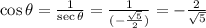
Rationalizing:
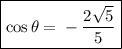
The sine can be calculated as: