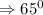Solution:
The formula for reference angle formula is
The first angle is given below as
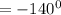
To figure out the quadrant under which it falls we will add 360 to it
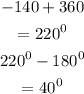
Hence,
-140 degrees fall under the THIRD QUADRANT as shown in the graph below
The reference angle for -140 degrees is
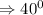
Part B:
The angle given is
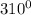
310 degrees fall under the 4th quadrant as shown in the image below
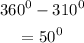
The reference angle for 310 degrees
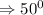
Part C:
The angle given here is
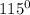
The sketch is given below as
As the angle falls under the SECOND QUADRANT
The reference angle for 115 degrees is