Question

Given the graph of a function f. Identify the function by name. Then Graph, state domain & range in set notation:A) f(x) +2B) f(x) -2

Answer 1

The function in the graph has the name of square function.

The domain of a function is all values of x the function can have. The domain of this function is all real numbers:

`\mleft\lbrace x\in\R\mright\rbrace`

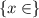
The range of a function is all values of y the function can have. The range of this function is all positive numbers, including zero:

`\mleft\lbrace y\in\R\mright|y\ge0\}`

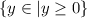
In order to graph f(x) + 2, we just need to translate the graph 2 units up. To find the new points, we need to increase all y-coordinates by 2:

(-2, 6), (-1, 3), (0, 2), (1, 3), (2, 6)

Domain: {x ∈ ℝ}

Range: y ∈ ℝ

Then, in order to graph f(x) - 2, we just need to translate the graph 2 units down. To find the new points, we need to decrease all y-coordinates by 2:

(-2, 2), (-1, -1), (0, -2), (1, -1), (2, 2)

Domain: {x ∈ ℝ}

Range: y ≥ -2