Question

g=9.8m/s2A block of mass m = 18 kg accelerates across a rough table when a force F = 100 N acts upon it at an angle = 35° with the horizontal. The force of friction on the block is f = 33 N.(a) What is the acceleration of the block? m/s2(b) What is the coefficient of friction of the block?

Answer 1

The free body diagram of the block can be shown as,

Part (a)

According to free body diagram, the net force which acts along x-axis is given as,

`F_x=F\cos \theta-f`

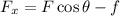
According to Newton's law, the net force acting along x-axis is,

`F_x=ma`

Plug in the known value,

`\begin{gathered} F\cos \theta-f=ma \\ a=(F\cos \theta-f)/(m) \end{gathered}`

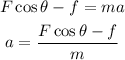
Substitute the known values,

`\begin{gathered} a=\frac{(100\text{ N)cos35-33 N}}{18\text{ kg}} \\ =\frac{(100N)(0.819)-33\text{ N}}{18\text{ kg}} \\ =\frac{48.9\text{ N}}{18\text{ kg}}(\frac{1kgm/s^2}{1\text{ N}}) \\ =2.72m/s^2 \end{gathered}`

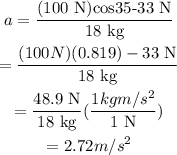
Thus, the acceleration of the block is 2.72 m/s2.

Part (b)

According to free body diagram, the net force acting along y-axis is,

`F_y=N+F\sin \theta-mg`

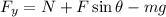
Since the block accelerates along x-axis therefore, the net force along y-axis is zero which can be expressed as,

`\begin{gathered} 0=N+F\sin \theta-mg \\ N=mg-F\sin \theta \end{gathered}`

Substitute the known values,

`\begin{gathered} N=(18\text{ kg)}(9.8ms^(-2))(\frac{1\text{ N}}{1kgm/s^2})-(100\text{ N)sin35} \\ =176.4\text{ N-}(100\text{ N)(0.574)} \\ =176.4\text{ N-}57.4\text{ N} \\ =119\text{ N} \end{gathered}`

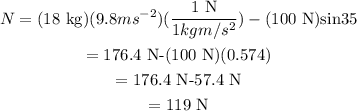
The formula to calculate the frictional force is,

`f=\mu N`

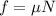
Substitute the known values,

`\begin{gathered} 33\text{ N=}\mu(119\text{ N)} \\ \mu=\frac{33\text{ N}}{119\text{ N}} \\ \approx0.277 \end{gathered}`

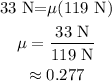
Thus, the coefficient of friction of block is 0.277.