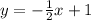The slope intercept form of a line equation is:

Where "m" is the slope and "b" is the y-intercept.
To create one line, we just need to choose values for "m" and "b", for example, let's pick m = 2 and b = 1.
Then the line is:

Every parallel line will have the same slope, so to find a different line that is paralle to it, we just need to maintain the same slope (the same "m") and change "b", for example, le'ts pick b = 2 now.
A parallel line is, then:
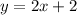
The slope of a perpendicular line can be found by inverting the slope and changin its sign, that is:

So, the slope of a line perpendicular to the original will be:
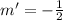
The "b" value can be any value and the line will still be perpencular. Le'ts pick b = 1 again.
So, a perpendicular line is:
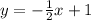
Original:

Parallel:
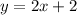
Perpendicular: