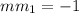Question

Prove: slope of AC x slope of DC = -1.

Answer 1

To find the slope, m, of a straight line, the formula is

`m=(y_2-y_1)/(x_2-x_1)`

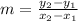
For line AC,

Picking coordinates from the graph

`\begin{gathered} (x_1,y_1)\Rightarrow(2,5) \\ (x_2,y_2)\Rightarrow(4,4) \end{gathered}`

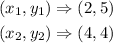
Substitute the coordinates into the formula to find the slope, m, of a straight line

`m=(4-5)/(4-2)=(-1)/(2)=-(1)/(2)`

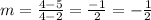
For line DC

Picking coordinates from the graph

`\begin{gathered} (x_1,y_1)\Rightarrow(4,4) \\ (x_2,y_2)\Rightarrow(6,8) \end{gathered}`

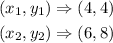
Substitute the coordinates into the formula to find the slope, m₁, of a straight line

`m=(8-4)/(6-4)=(4)/(2)=2`

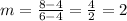
Line AC and DC are perpendicular, i.e.

`m* m_1=-(1)/(2)*2=-1`

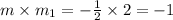
Hence,

`mm_1=-1`