Question

Write a formula for the function in the image below. When typing exponents use the carrot key ^ by pressing SHIFT and 6. For example x squared can be typed as x^2. Do not put spaces between your characters and remember to use parentheses in the appropriate places!quadratic/parabola opening up with vertex at (1,-3)The new equations f(x)=Answer

Answer 1

The equation of a parabola with vertex (h,k) is:

`f(x)=c(x-h)^2+k`

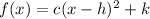
Where c is a constant.

Notice that the graph of this parabola has a y-intercept of -2 and the vertex has coordinates (1,-3). Replace h=1 and k=-3:

`f(x)=c(x-1)^2-3`

Since f(0)=-2, replace x=0 and f(0)=-2 to find the value of the constant c:

`\begin{gathered} f(0)=c(0-1)^2-3 \\ \Rightarrow-2=c-3 \\ \Rightarrow c=3-2 \\ \Rightarrow c=1 \end{gathered}`

Then, the equation for the given graph, is:

`f(x)=(x-1)^2-3`

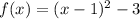
Which can be expanded as follows:

`\begin{gathered} f(x)=x^2-2x+1-3 \\ \Rightarrow f(x)=x^2-2x-2 \end{gathered}`

Therefore, two possible (equivalent) answers are:

f(x) = x^2-2x-2

f(x) = (x-1)^2-3