We have the following inequality,
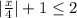
By subtracting 1 to both sides, we have

From the absolute value properties, this inequality can solved in 2 cases:
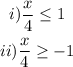
Case i).
By multiplying both sides by 4, we have
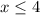
Case ii)
Similarly, by multiplying both sides by 4, we get
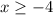
Therefore, the answer is the intersection of both results, that is,
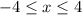
Then, the answer is option A.