We are given that a 20 kg object moves a distance of 12 meters. The intial velocity is 10 m/s. To calculate the friction force we will use the fact that the chage in the kinetic energy is equal to the work done by the frictio force, therefore, we have:
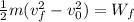
Where:
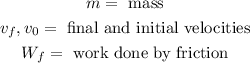
Now, we plug in the values:
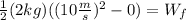
Solving the operations:
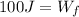
Now, the work done by friction is equal to the friction force multiplied by the distance:
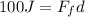
Now, we divide both sides by the distance:
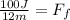
Solving the operations:
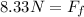
Therefore, the force of friction is 8.33 Newtons.