Question

Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.Anthony plans to attend the Hancock County Fair and is trying to decide what would be a better deal. He can pay $39 for unlimited rides, or he can pay $12 for admission plus $1 per ride. If Anthony goes on a certain number of rides, the two options wind up costing him the same amount. What is that cost? How many rides is that?

Answer 1

Given data:

$39 for unlimited rides

$12 for admission plus $1 per ride

Let x be the number of rides

Let y be the cost in terms of the number of rides

First option is always $39 (it doesn't depend of the number of rides)

`y=39`

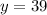
Second option is $12 plus $1 multiplied by the number of rides:

`y=12+1x`

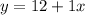
System of equations:

`\begin{gathered} y=39 \\ y=12+x \end{gathered}`

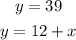
The two options wind up costing the same amount when the equations are equal:

y=y

Subtitute the value of y corresponding in each equation:

`39=12+x`

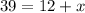
Solve x:

`\begin{gathered} 39-12=12-12+x \\ 27=x \\ \\ x=27 \end{gathered}`

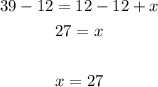
Then, the two options wind up costing the same amount at $39 and it correspond to 27 rides