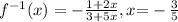Answer::
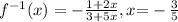
Explanation:
We want to find the function that corresponds to the inverse function:
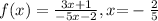
To do this, we find the inverse of f(x).
In order to find the inverse of f(x), follow the steps below:
Step 1: Replace f(x) with y:
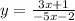
Step 2: Swap x and y
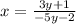
Step 3: Make y the subject of the equation:
![\begin{gathered} \text{ Cross multiply} \\ x(-5y-2)=3y+1 \\ \text{ Open the bracket on the left side:} \\ -5xy-2x=3y+1 \\ \text{ Bring all the terms containing y to one side of the equation.} \\ -5xy-3y=1+2x \\ \text{ Factor out y} \\ y(-5x-3)=1+2x \\ \text{ Divide both sides by }-5x-3 \\ y=(1+2x)/(-5x-3) \end{gathered}]()
Step 4: Replace y the inverse of f(x).
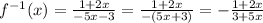
The function that corresponds to the given inverse function is: