Divide the traveled distance over the time it takes to travel it to find the speed as a unit rate. Then, compare with other unit rates to find if they are equivalent.
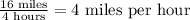
A)
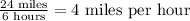
B)

C)
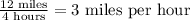
D)
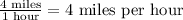
Notice that the ratios given in the options A and D are equivalent, but those in B and C are not.