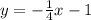The point-slope form is as follows:

Where m is the slope and (xP, yP) is a point on the line. We can use any opint as long as it is on the line.
The slope-intercept form is:

Where m is the same slope and b is the y-intercept. We can find it by either using the y-intercept or by solving the slope-point form for y.
First, we need to find the slope using the points (4, -2) and (-8, 1):
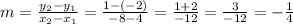
So, to find the point-slope form, we can use either points, so let's use (4, -2):
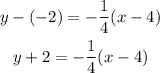
And to find the slope-intercept, we just solve the parenthesis and solve for y:

So, one of the possible point-slope forms is:
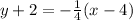
And the slope-intercept form is: