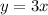the equations for the two lines:
1. First line:
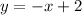
2. Second line:
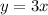
To write the equation of a line in slope-intercept form
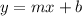 , we need two things:
, we need two things:
1. The slope
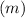 of the line, which can be calculated using two points on the line with the formula
of the line, which can be calculated using two points on the line with the formula
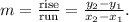
2. The y-intercept
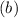 , which is the value of
, which is the value of
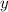 where the line crosses the y-axis
where the line crosses the y-axis
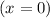 .
.
For the first image, using the points (2,0) and (0,2):
1. Calculate the slope
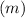 :
:
![\[ m = (2 - 0)/(0 - 2) = (2)/(-2) = -1 \]](https://img.qammunity.org/2023/formulas/mathematics/college/c4pjmgdvsorq8uhn0aphim0b883ynvmgny.png)
2. Since the line crosses the y-axis at (0,2), the y-intercept
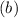 is 2.
is 2.
Therefore, the equation of the line for the first image is:
![\[ y = -x + 2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/k9vuex9l73yefq4ksmmtcyjp5lbwo3k0gf.png)
For the second image, using the points
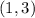 and
and
 :
:
1. Calculate the slope
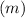 :
:
![\[ m = (-3 - 3)/(-1 - 1) = (-6)/(-2) = 3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/zarsa6tiphqygzmmoluhckb4t2tm2v9hzp.png)
2. To find the y-intercept
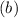 , we can use the point (1,3) and the slope we just calculated. Plugging the point into the slope-intercept form gives us:
, we can use the point (1,3) and the slope we just calculated. Plugging the point into the slope-intercept form gives us:
![\[ 3 = 3(1) + b \]](https://img.qammunity.org/2023/formulas/mathematics/college/omo2lh0onltrkvk1s4trg627epizk5lvkd.png)
![\[ b = 3 - 3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/gnce63dlmgip95oedtx6rvi2bl23lcxqb4.png)
![\[ b = 0 \]](https://img.qammunity.org/2023/formulas/mathematics/college/oqflkxmdt1k1mnwudrvmkhg53xr86gjghm.png)
Therefore, the equation of the line for the second image is:
![\[ y = 3x \]](https://img.qammunity.org/2023/formulas/mathematics/college/380mj5xwgb8lhbof69jubcxyjohsm78e8w.png)
So we have the equations for the two lines:
1. First line:
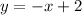
2. Second line: