The behavior of the data are almost linear. Hence, a good prediction can be modeled by a straight line.
From the graph, we can take 2 points. For instance (0,333) and (40,354).
Hence, the slope of the approximate line is
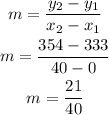
Then, the approximate line has the form

where b is the y-intercept. This can be obtained by substituying the point (0,33) into the last equation, it yields

and the approximate line equation is
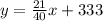
By means of this equation we can predict another point. For instance, when the air temperature is x=50, we have
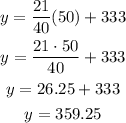
Therefore, the best aproximation for the speed of sound is y=360 m/s